Graph Traversal

Graph traversal algorithms visit all nodes within a graph in a certain order to compute info along the way. DFS and BFS are two common algos for doing this.

Connected component: two nodes are in the same connected component if they can reach each other. For undirected graphs.

DFS

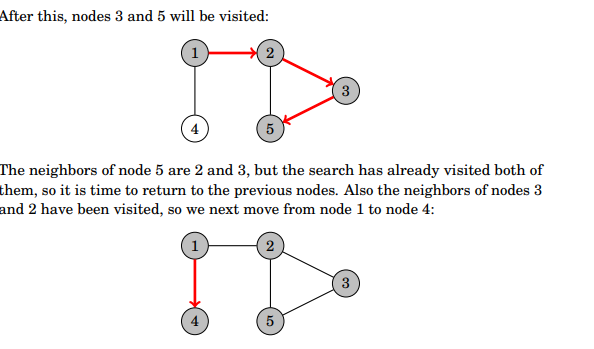
It begins at a starting node and goes to all the other reachable nodes using the edges (connecting lines) of the graph. It goes through one path at a time. The time complexity of O(n + m) where n is the number of nodes and m is the number of edges. Code for DFS:

// Adjacency list representation of graph
vector <int> adj[N];
bool visited[N];

void dfs (int s)
{
	if (visited[s]) return;
	visited[s] = true;
	//process node s
	...
	//process all the nodes s is linked to
	for (auto u: adj[s])
	{
		dfs(u);
	}
}

BFS

Visits the nodes in increasing order of distance from the starting node. Goes one level after another.

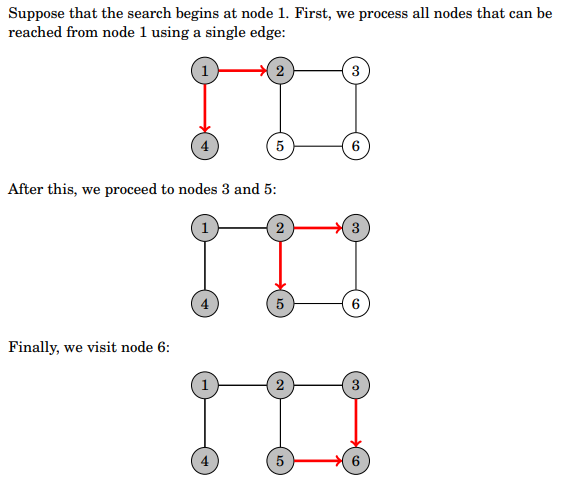
The time complexity of BFS is O(n+m) where n is the number of nodes and m is the number of edges.

// The queue contains nodes to be processed in increasing order of distance. New nodes are added to the end and the node at the beginning of the queue is the next node to be processed.
queue <int> q;
bool visited[N];
int distance [N];

//Start is at node x
visited[x] = true;
distance[x] = 0;
q.push(x);
while (!q.empty())
{
	int s = q.front();
	q.pop();
	//Process node s
	...
	for (auto u : adj[s])
	{
		if (visited[u]) continue;
		visited[u] = true;
		distance[u] = distance[s] +1;
		q.push(u);
	}
}

You need to use a Queue for bfs.

Applications of Graph Traversal Algos

It’s usually better to use dfs because it’s easier to implement than bfs.

Common use cases for undirected graphs:

1. Checking for connectivity in the graph. A graph is connected if you can start at any node and end up at any other node. You can check if a graph is connected by starting at a random node and finding out if you can reach all the other ones.
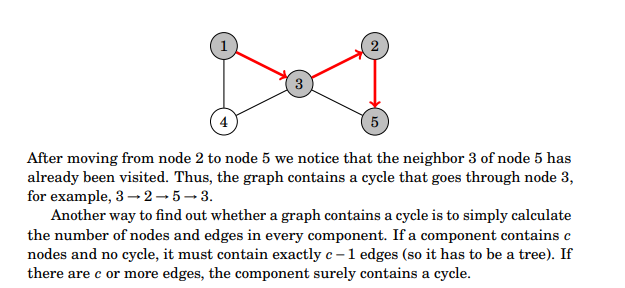
2. Finding cycles: A cycle is when you find a neighbor other than the previous node that’s already been visited.
3. Bipartiteness check: A graph is bipartite if its nodes can be colored using two colors such that there are no adjacent nodes with the same color. The way you check it is coloring node 1 blue, all its neighbors red, all their neighbors blue, and so on. If there are two adjacent nodes that have the same color, it’s not bipartite.

competitive_programming