1D Prefix Sums
Let’s say that you have a one-indexed integer array arr of size N, and you want to compute the value of arr[a] + arr[a+1] + … + arr[b] for Q different pairs within arr.
In bronze, you would just brute force and iterate through all entries from index a - index b and add them up. But this take O(NQ) because each query would take O(N) time. In most silver+ problems, this wouldn’t be acceptable.
Prefix sums can speed up the operation. Create a prefix sum array prefix. Set prefix[0] = 0 (because you’re 1-indexing the array), and then for indices k, 1 ⇐ k ⇐ N, the prefix sum array is:
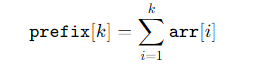 This means that every element stores the sum of all the elements in the original array from index 1 to k. You can do this in O(N).
This means that every element stores the sum of all the elements in the original array from index 1 to k. You can do this in O(N).
Now you can run thru the queries by doing prefix[b] - prefix[a-1]. Running through all the queries will take O(Q). The overall process will take O(N+Q), which is significantly faster.
2D Prefix Sums
If you want to process Q queries for the sum of subrectangles of 2d matrices with N rows and M columns, it would take O(QNM) time if you iterate naively. This is too slow for most problems.
You can optimize this to O(QN) by creating a simple prefix array for each row.
You can further optimize this by doing 2d prefix sums. The prefix sum can be calculated as follows for row i and column j, where i and j are 1-indexed.
The submatrix sum between rows a and A and columns b and B, can be expressed as:
We only need to access 4 values for an submatrix, which means that this solution will run in O(Q) time after a processing of O(NM) time.